误差

第一题

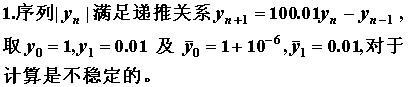
image-20220924232308612

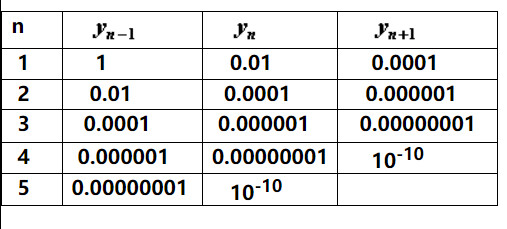
直接带入计算，观察$y_{n+1}、y_{n}、y_{n-1}$的关系，判断以该公式计算是否稳定

image-20220924225646620

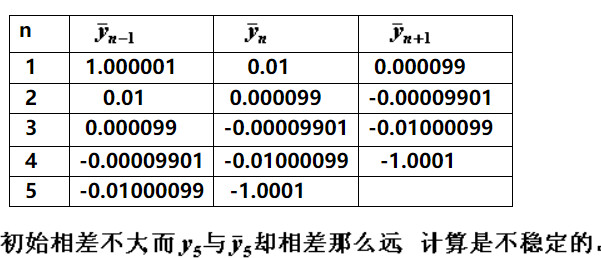
image-20220924225654960

第三题

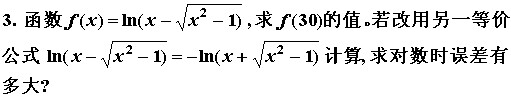
image-20220924232344070

对应原书中内容：1.3 函数的误差估计

函数套函数的类型，将两层函数分别表示出后：

  • 计算出第二层函数的值，计算出$y^*$后，确定出$|E(y)|$的位数
  • 不知道算出的$z^*$有什么用
  • 计算出导数的绝对值$|z’|$
  • 计算出$|E(z)| = |z’||E(y)|$的值，作为误差的判别标准

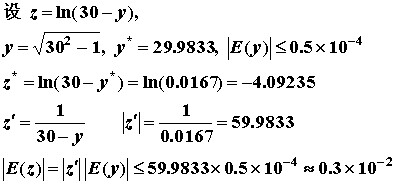
image-20220924232355967

image-20220924232400779

第五题

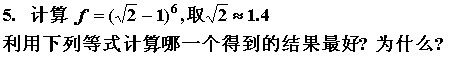
image-20220924232417210

image-20220924232429170

对应原书中内容：1.4 近似数的四则运算及数值计算中需注意的几个问题

尽量避免：

  • 加减运算：
    • 避免两个绝对值差不多的数相互抵消
    • 不要把绝对值差异很大的数做加减法
  • 乘除运算：
    • 避免除数接近于0
  • 舍入误差的积累：
    • 减少运算次数
    • 简化步骤

第六题

image-20220924232145430

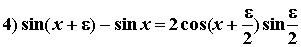
image-20220924232453670

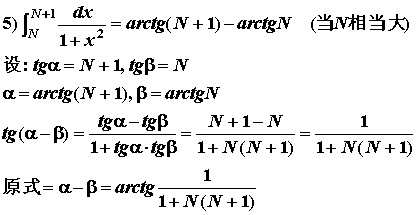
image-20220924232459419

第十题

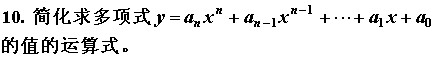
image-20220924232550199

对应原书中内容：2.1.1 多项式

秦九韶算法

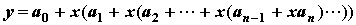
image-20220924232601806

非线性方程求根

多项式及代数方程根的界

笛卡尔符号法则

image-20220925093328108

正根上界

image-20220925093435667

二分法

估计二分法的执行次数$K$

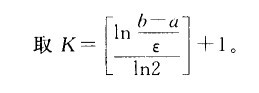
image-20220925093602315

其中：

  • $b-a$为最初的两个点的值
  • $\epsilon$为指定出的精度，如精确到小数点后一位为$0.5\times10^{-1}$
  • 其他部分为固定数值

由于最初选定的两个点的不同，$K$的值会有变化

例题

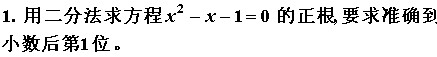
image-20220925094451874

使用笛卡尔符号规则：

image-20220925094520224

由序列${1、-1、-1}$可知变号1次，无法少一个正偶数，则必定有一个正根

由序列${1、1、-1}$可知变号1次，无法少一个正偶数，则必定有一个负根

使用正根上界：

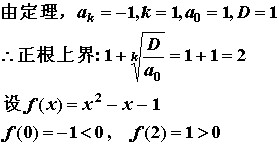
image-20220925094541924

估算$K$值：

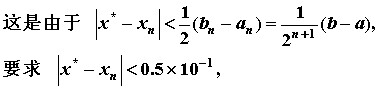
image-20220925094631336

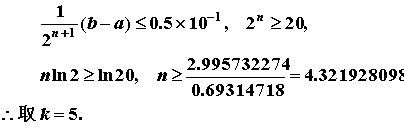
image-20220925094659516

这里发生了错误，根据原题目中例子这里取了$b-a = 2$，则计算出的$K$应为6

在得知计算次数为6次后，列表计算：

$a$ $b$ $x=(a+b)/2$ $f(a)$ $f(b)$ $f(x)$
0 2 1 -1 1 -1
1 2 1.5 -1 1 -0.25
1.5 2 1.75 -0.25 1 0.3125
1.5 1.75 1.625 -0.25 0.3125 0.015625
1.5 1.625 1.5625 -0.25 0.015625 -0.121094
1.5625 1.625 1.59375

其中保留的是与$f(x)$异号的一项再次进行迭代计算

第六次计算出的区间的中位数即通过二分法估算出的方程的解

简单迭代法

等价方程

image-20220925101208328

等价方程不止一种形式

收敛性

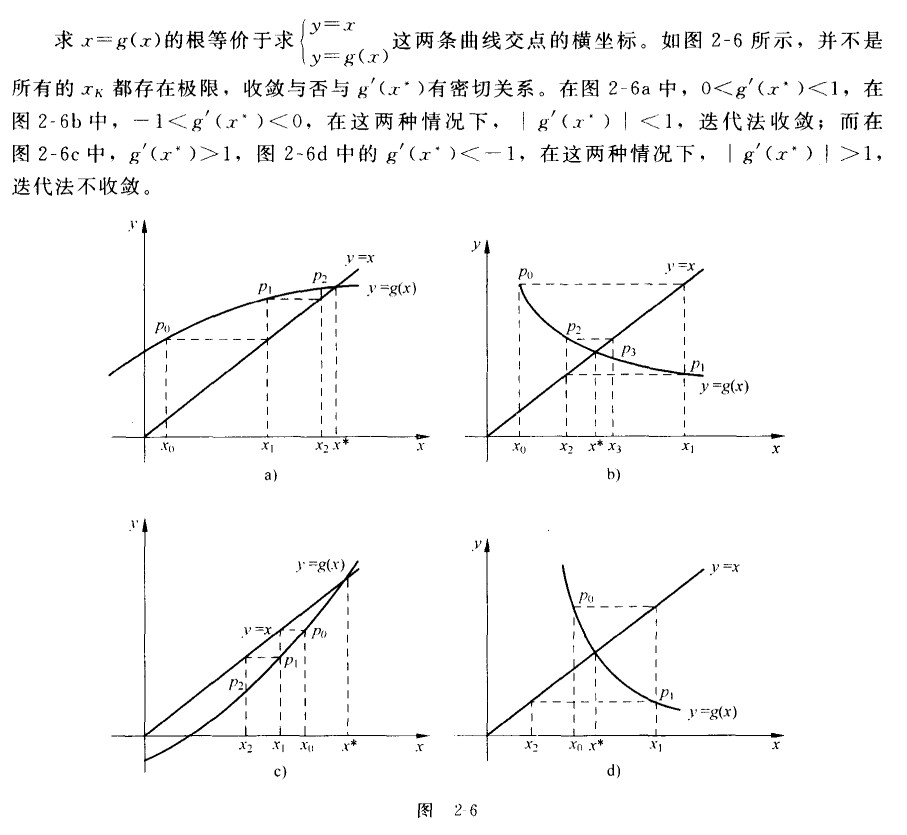
image-20220925101324832

根据等价方程的导数在可行域的绝对值判断其是否收敛：

  • $|g’(x^*)| < 1$，迭代法收敛
  • $|g’(x^*)| > 1$，迭代法发散

与二分法的对比

image-20220925102015922

$L$为渐进收敛因子

例题

image-20220925104844805

image-20220925104851588

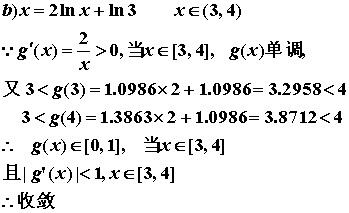
image-20220925104858482

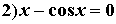
image-20220925104904767

image-20220925104910236

image-20220925104917937

收敛时需要保证：

  • 对于选取的等价方程需要满足于特定作用域，方法为证明其单调性，并通过极值判断出取值范围
  • 保证等价方程的导数的绝对值小于1

关于如何确定范围：

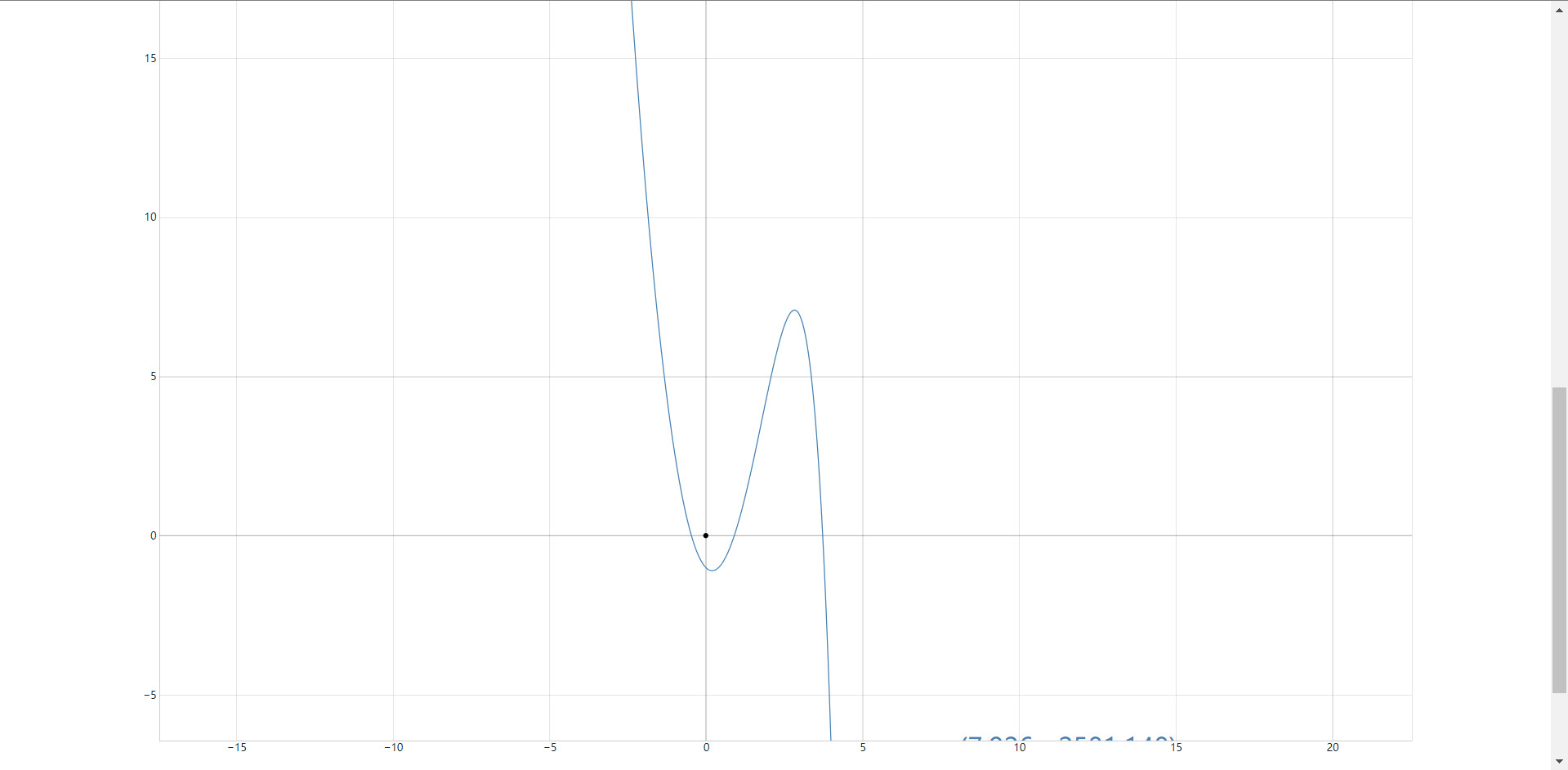
image-20220925105332994

第一题图像如图所示

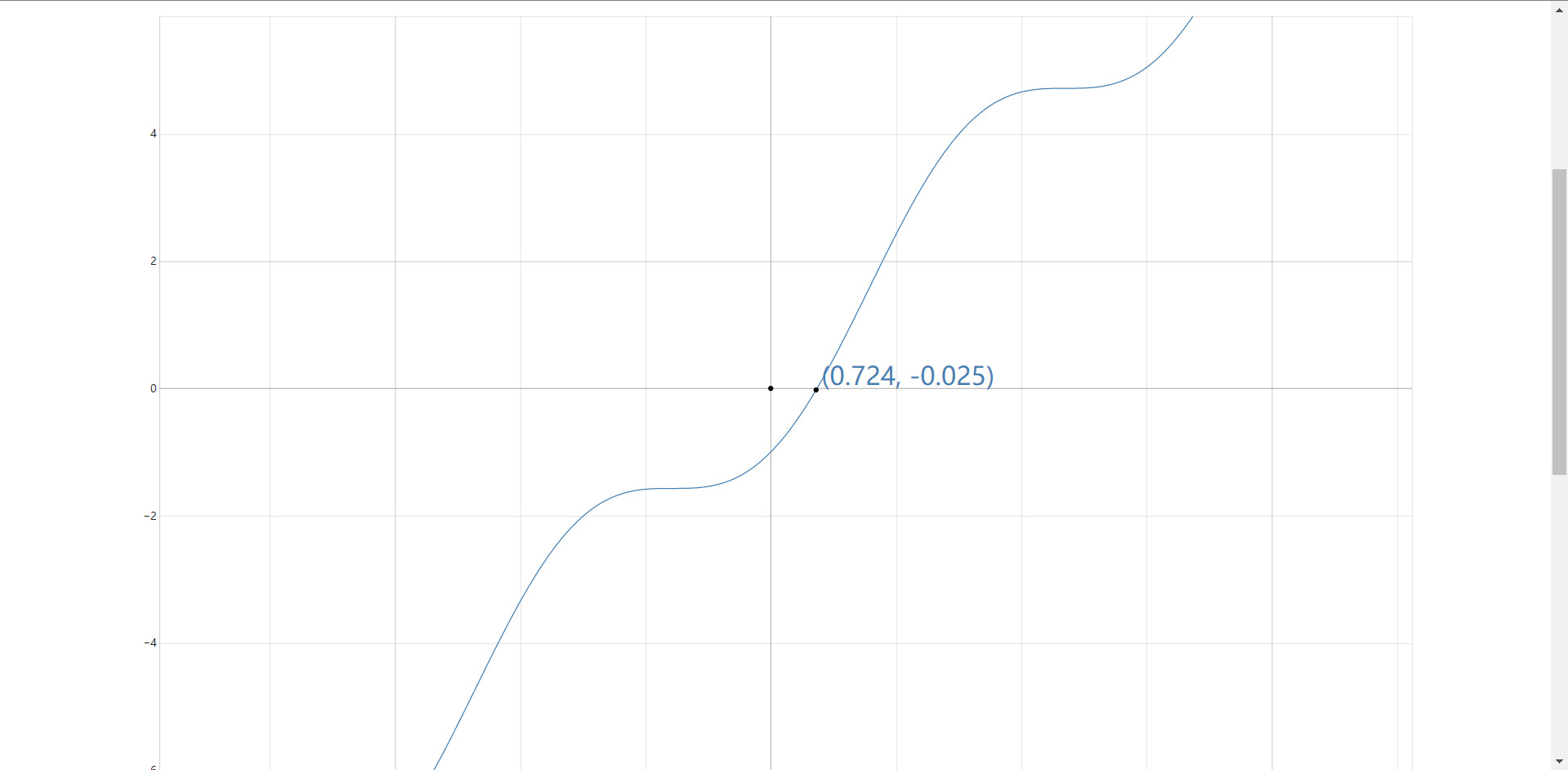
image-20220925105407119

第二题图像如图所示

选取区间时只需要大概地判断出即可

牛顿法

计算步骤

image-20220925144625058

只需要记住牛顿法的迭代公式即可
$$
x_{k+1} = x_k - \frac{f(x_k)}{f’(x_k)}
$$

例题

image-20220925144818203

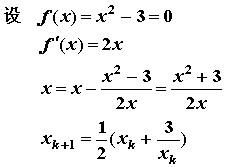
image-20220925144824108

根据公式计算出公式后直接计算即可

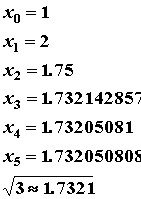
image-20220925144954123

只要出现结果停止变化的情况就可以停止计算

收敛性判断

image-20220925151225176

满足以上几点就可以证明收敛

例题

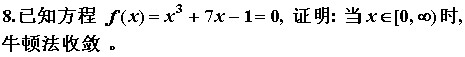
image-20220925151327707

image-20220925151338363

解线性方程组的直接法

【计算方法】零基础入门矩阵1（第五期）矩阵消去法 全主元 列主元 三角分解 LU分解 PLU分解_哔哩哔哩_bilibili

高斯消元法

全主元法

image-20220925170235267

  • 从A中选取绝对值最大的数作为主元
  • 交换行列，让主元位于$a_{11}$位置，这步可以忽略
  • 消元计算
  • 在A中的第N-K+1行、列选取下一个主元，选取标准为这些数的最大值，且不与之前的主元处于同一行
    • N：行数
    • K：消元次数
  • 交换行列，让主元位于$a_{11}$位置，这步可以忽略
  • 重复消元计算，直到所有行都存在主元

列主元法

image-20220925170706166

与全主元法规则类似，只是主元的选取标准改变为从每一列中选取一个

三角分解法

道立特分解法

【计算方法】零基础入门矩阵1（第五期）矩阵消去法 全主元 列主元 三角分解 LU分解 PLU分解_哔哩哔哩_bilibili

【数值分析】矩阵LU三角分解| 速成讲解 考试宝典_哔哩哔哩_bilibili

需要将方程组表示为矩阵的形式后

将A分解为L和U的形式，A=LU，其中L是单位下三角矩阵，主对角线全为1，U是上三角矩阵

image-20220925190238424

首先按照消元法求出U，后根据求取U时的列向量减系数填补出L

image-20220925190432168

对于$a_{11} = 0$的情况，需要进行PLU分解，即在A=LU的等式前左乘一个P，组成PA=LU

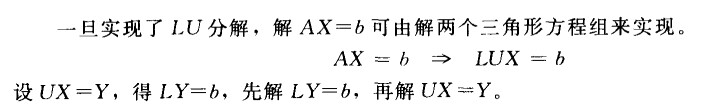
image-20220925190705927

根据分解出的LU列出UX=Y、LY=b的式子，后分别求取其中结果

平方根法公式求解

cholesky分解简单速成_哔哩哔哩_bilibili

对于正定矩阵：

  • 对称的
  • 特征值都大于0的

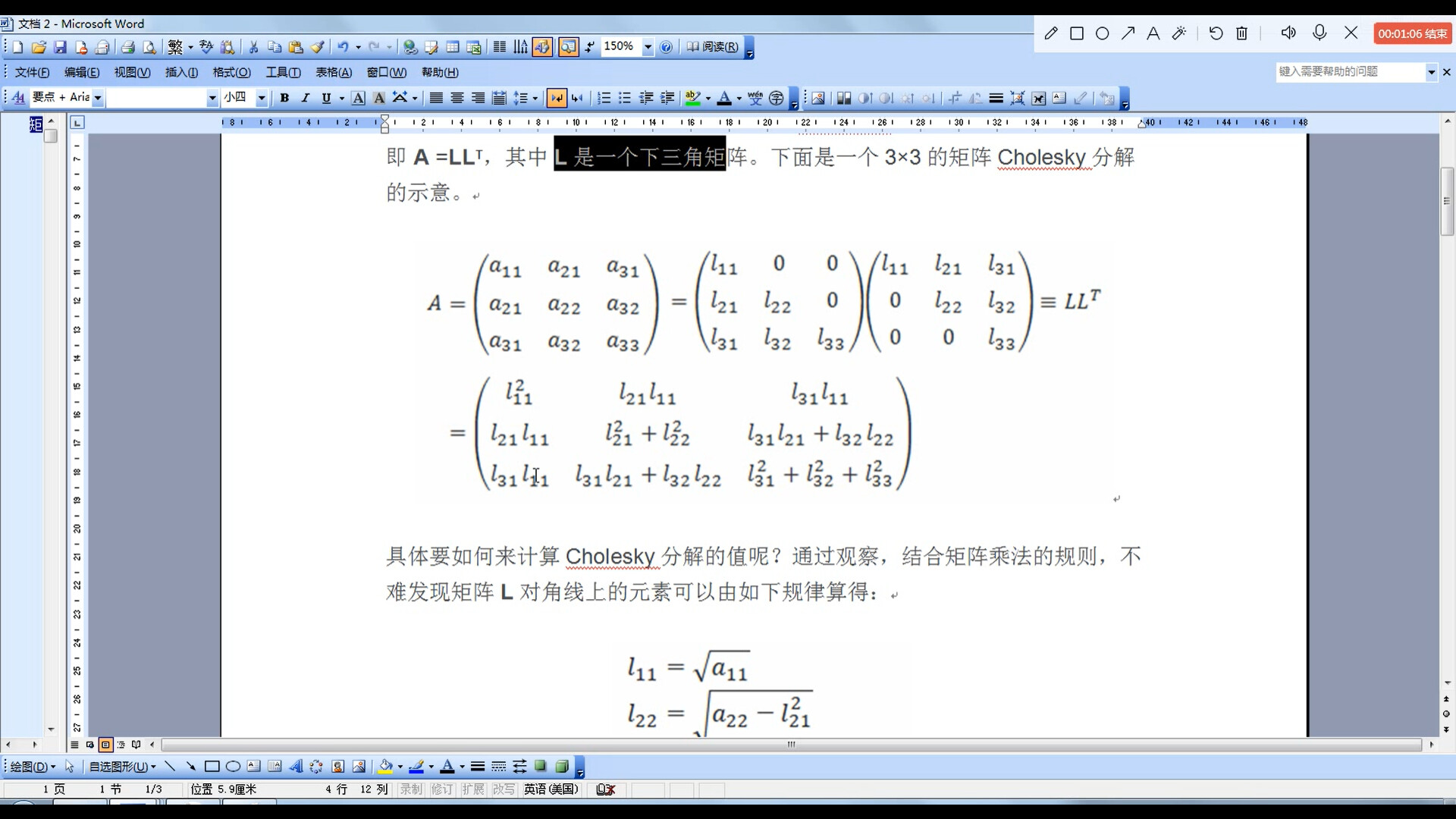
image-20220925190924785

将其分解为一个矩阵和其转置矩阵的乘积，其中对应的映射关系如图所示

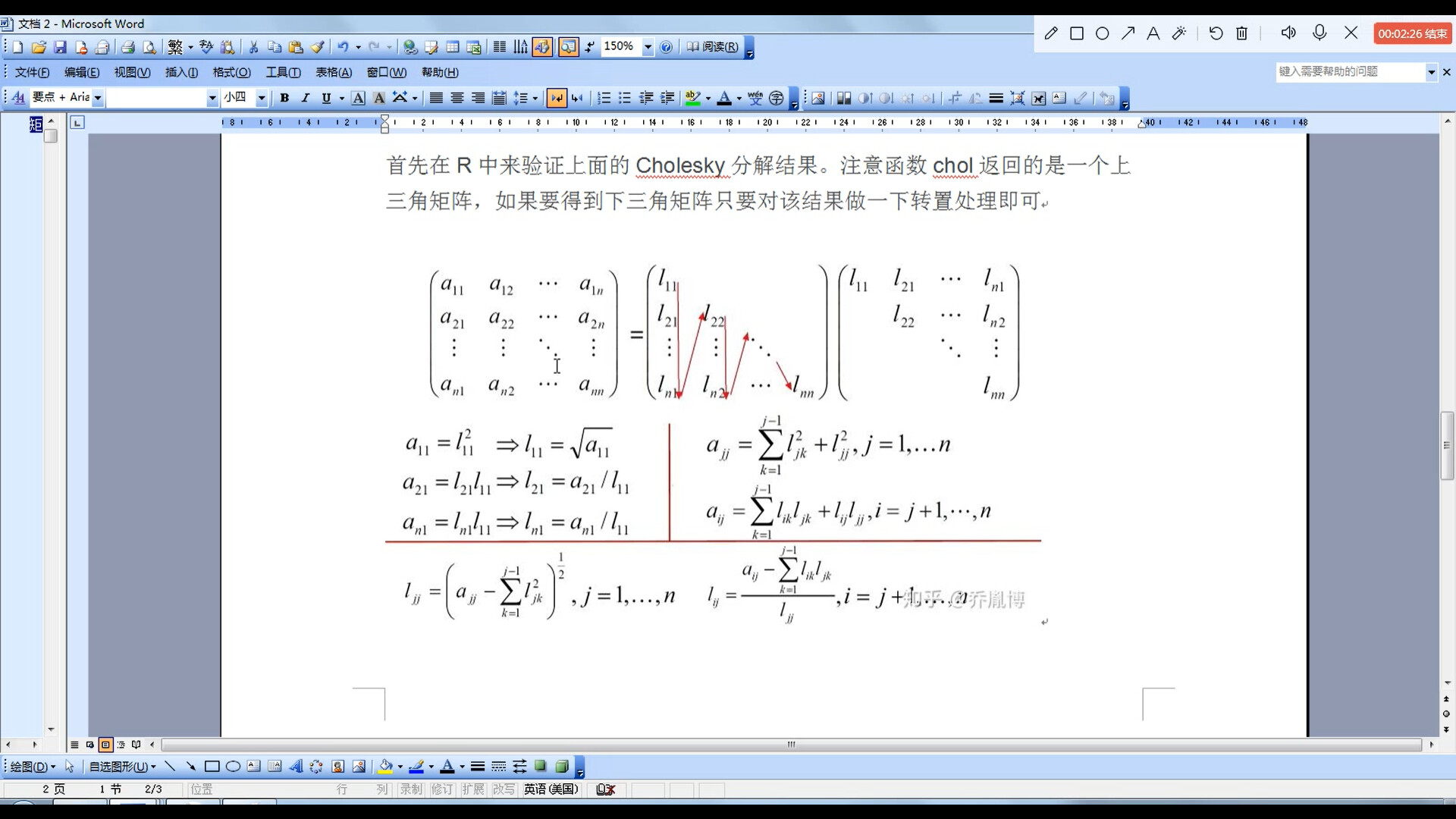
image-20220925191130123

其计算方式是按列来的

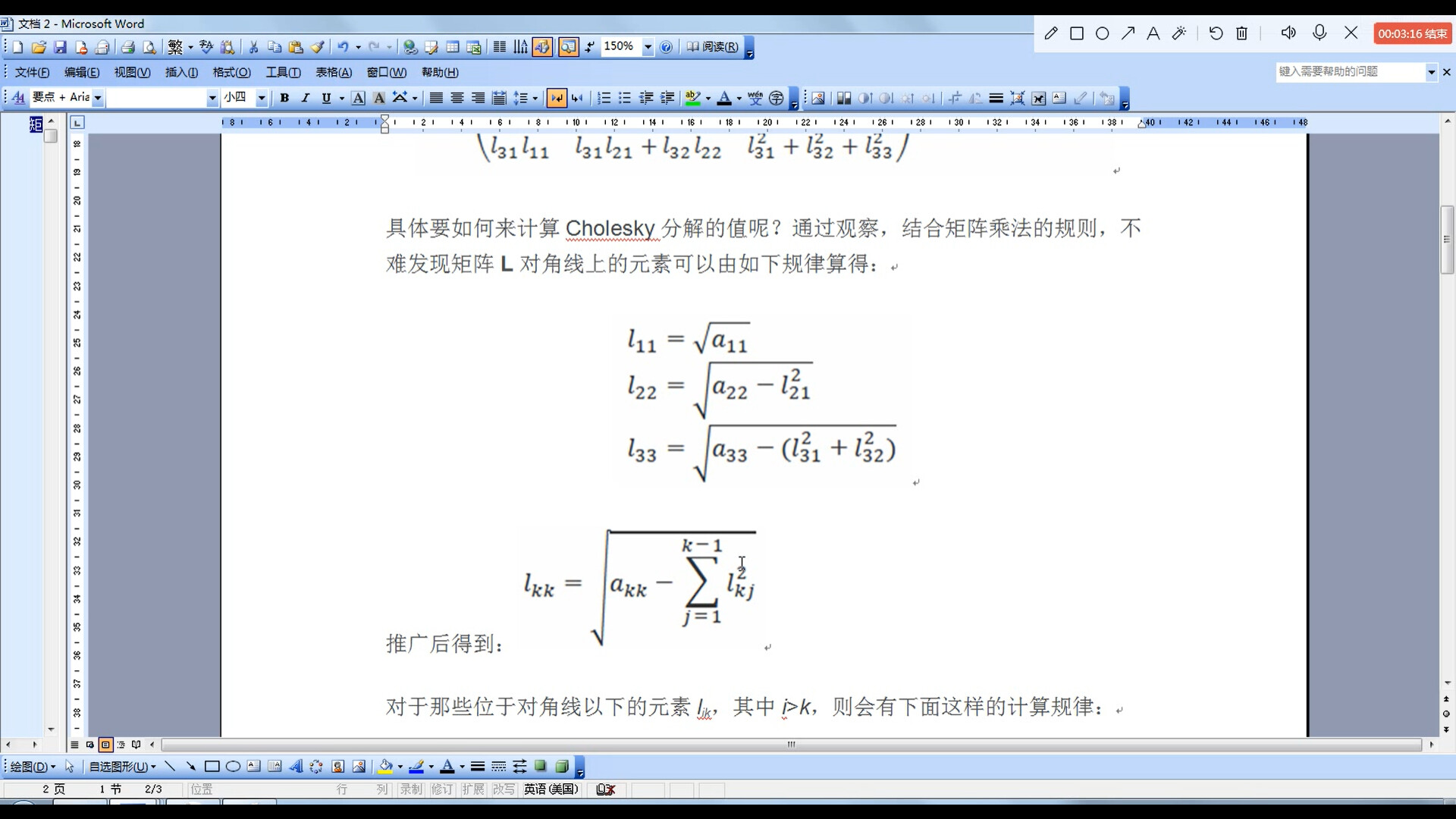
image-20220925191431039

其中对角线上的元素规律如图所示

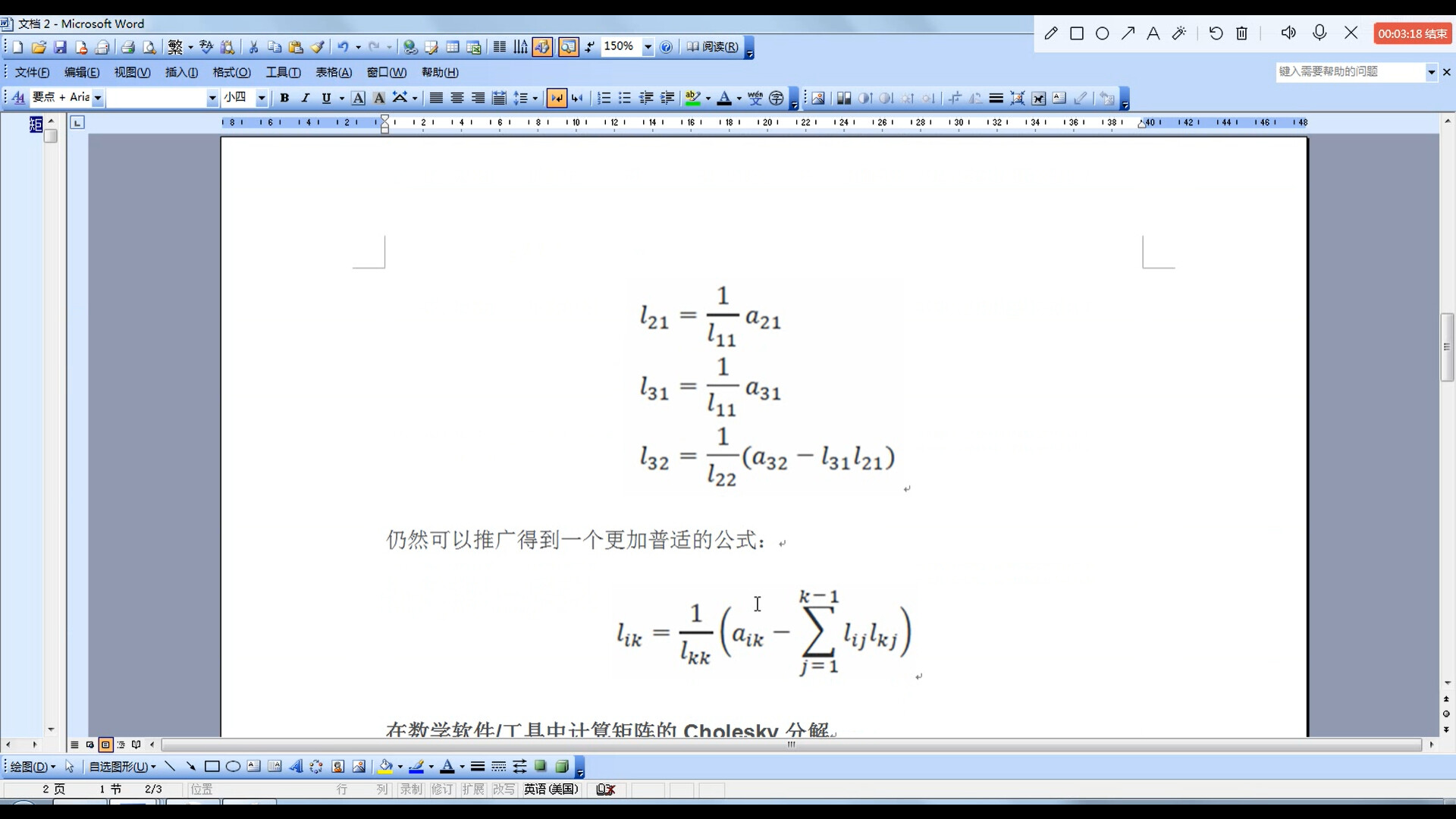
image-20220925191457506

对角线元素下的元素规律如图所示

例题

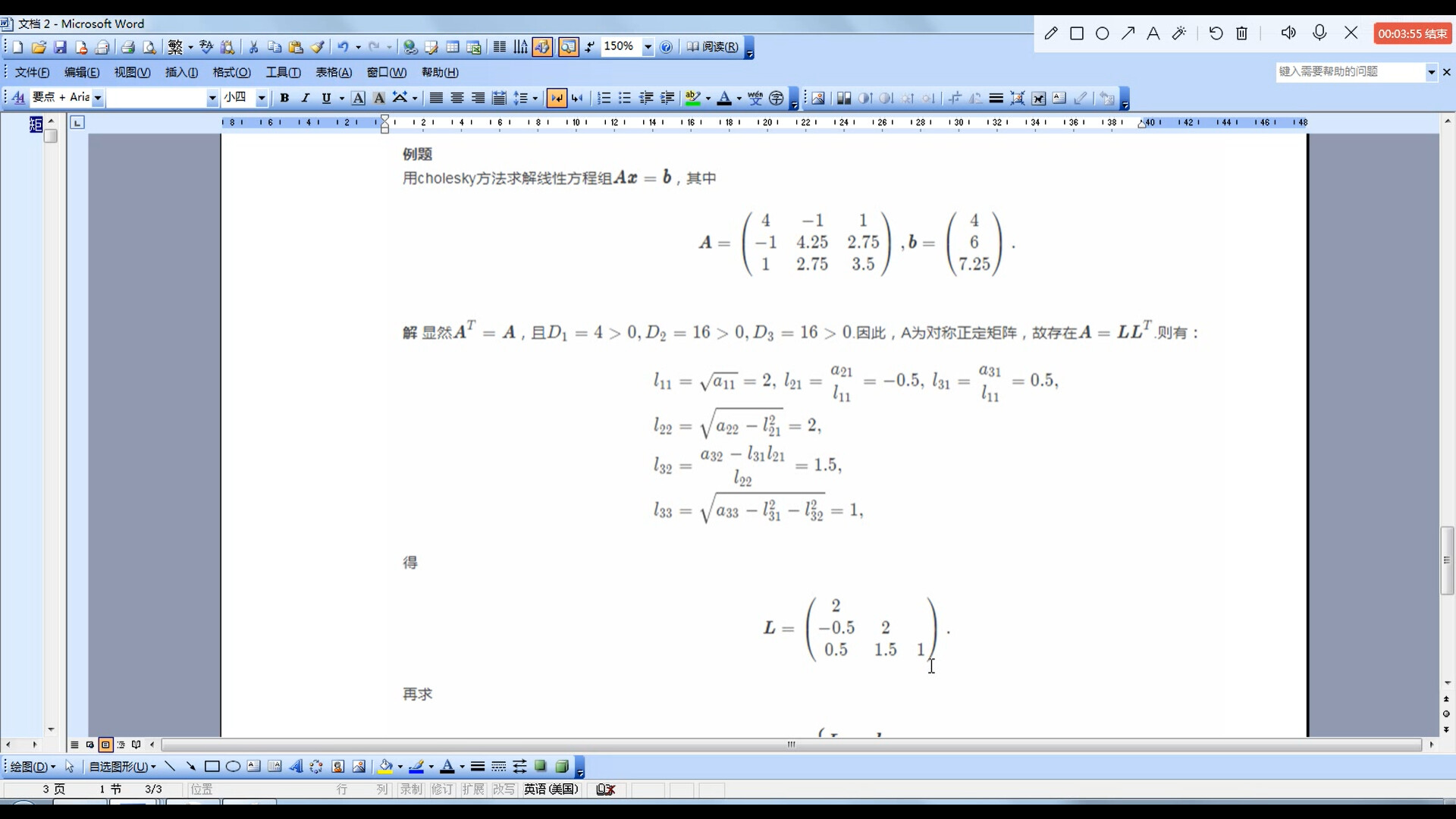
image-20220925191224941

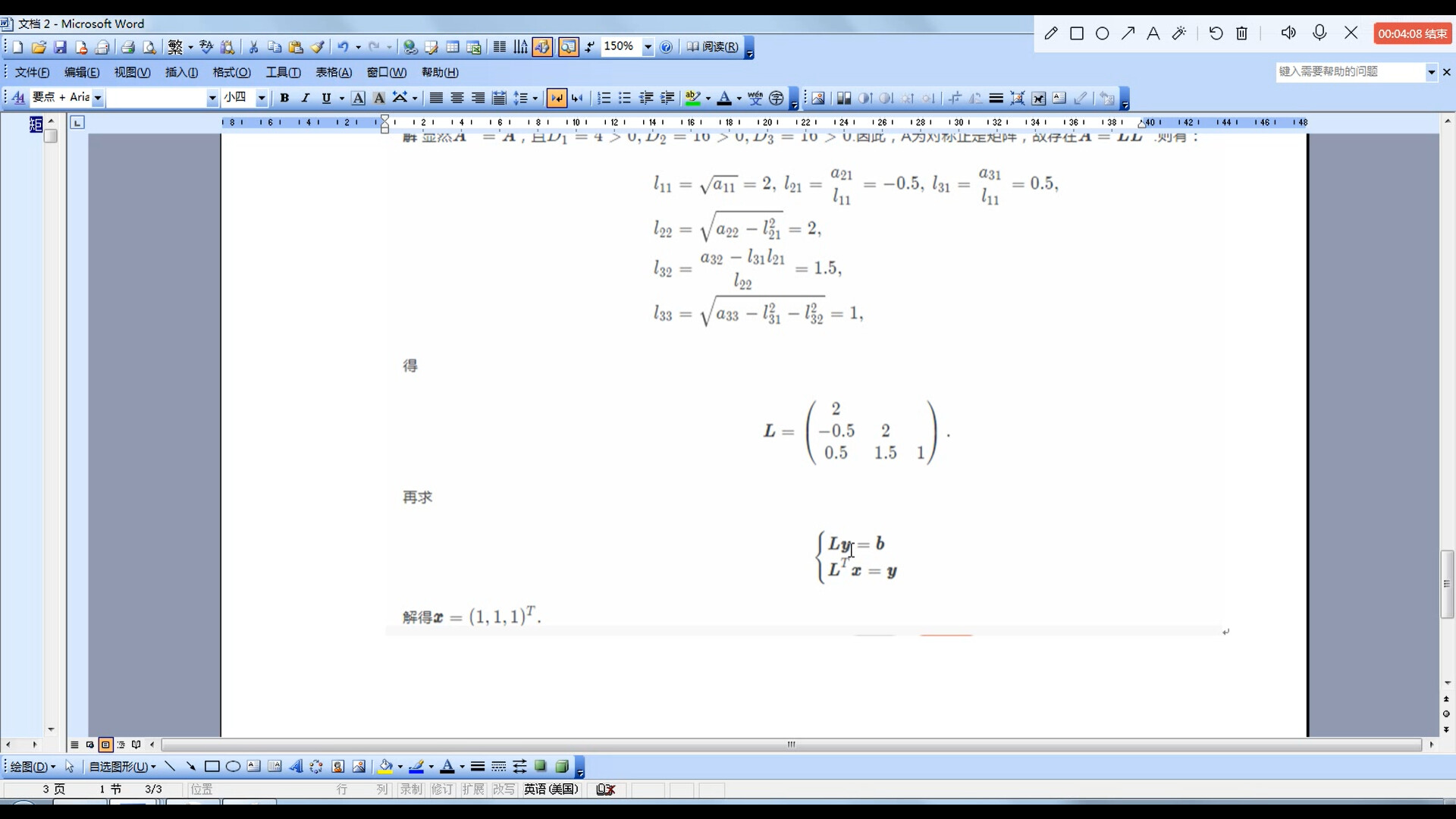
image-20220925191606471

求出$A = L^TL$后，按照$Ly = b$、$L^Tx = y$的式子求出最后$x$的结果
$$
\begin{cases}
Ly = b \
L^Tx = y \
\end{cases}
$$

平方根法

【数值分析】矩阵三角分解｜速成平方根法和追赶法 解线性方程组_哔哩哔哩_bilibili

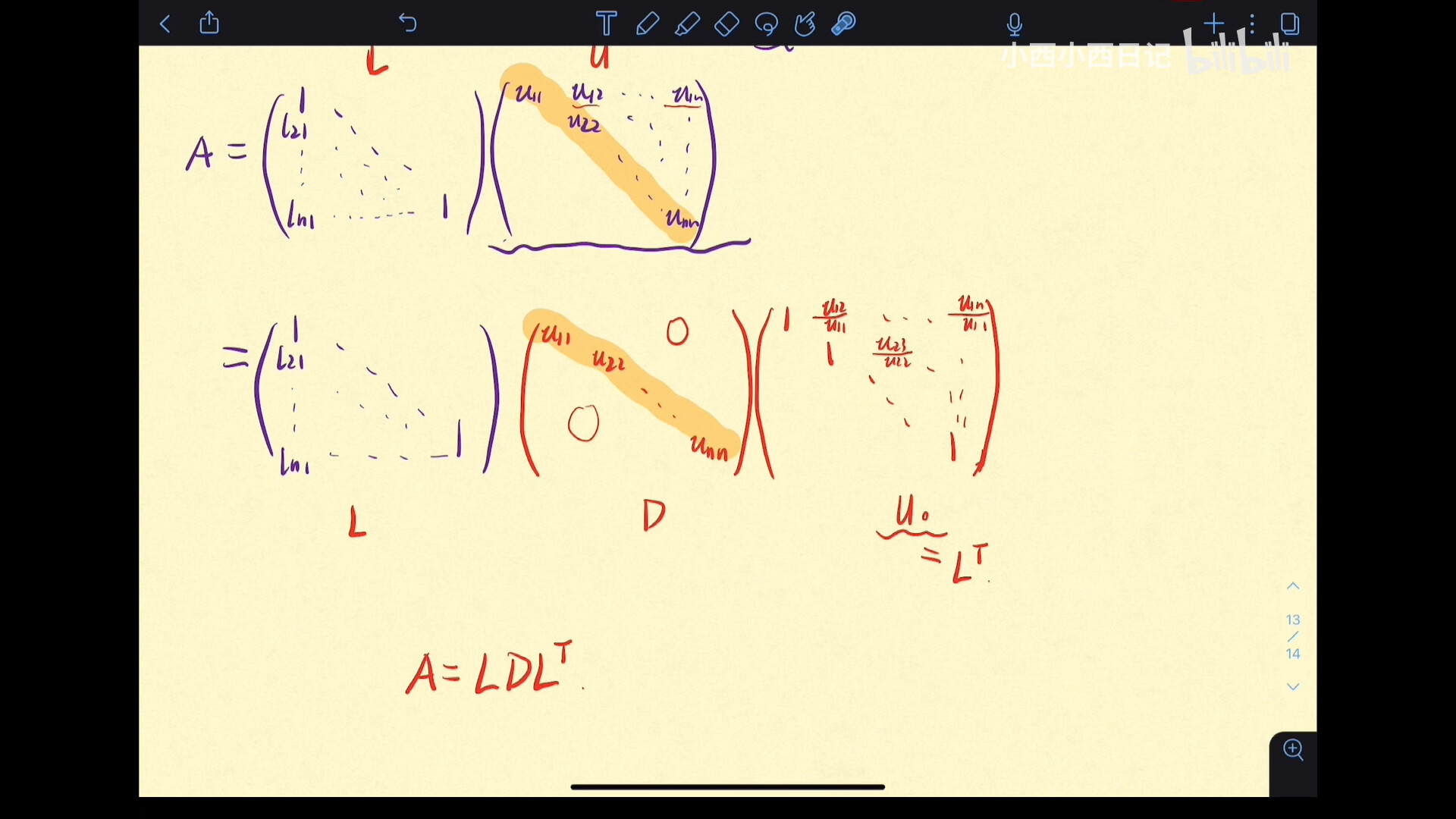
image-20220925203039218

A=LU在A是正定矩阵的情况下具有如上性质：可将U表示为$DL^T$

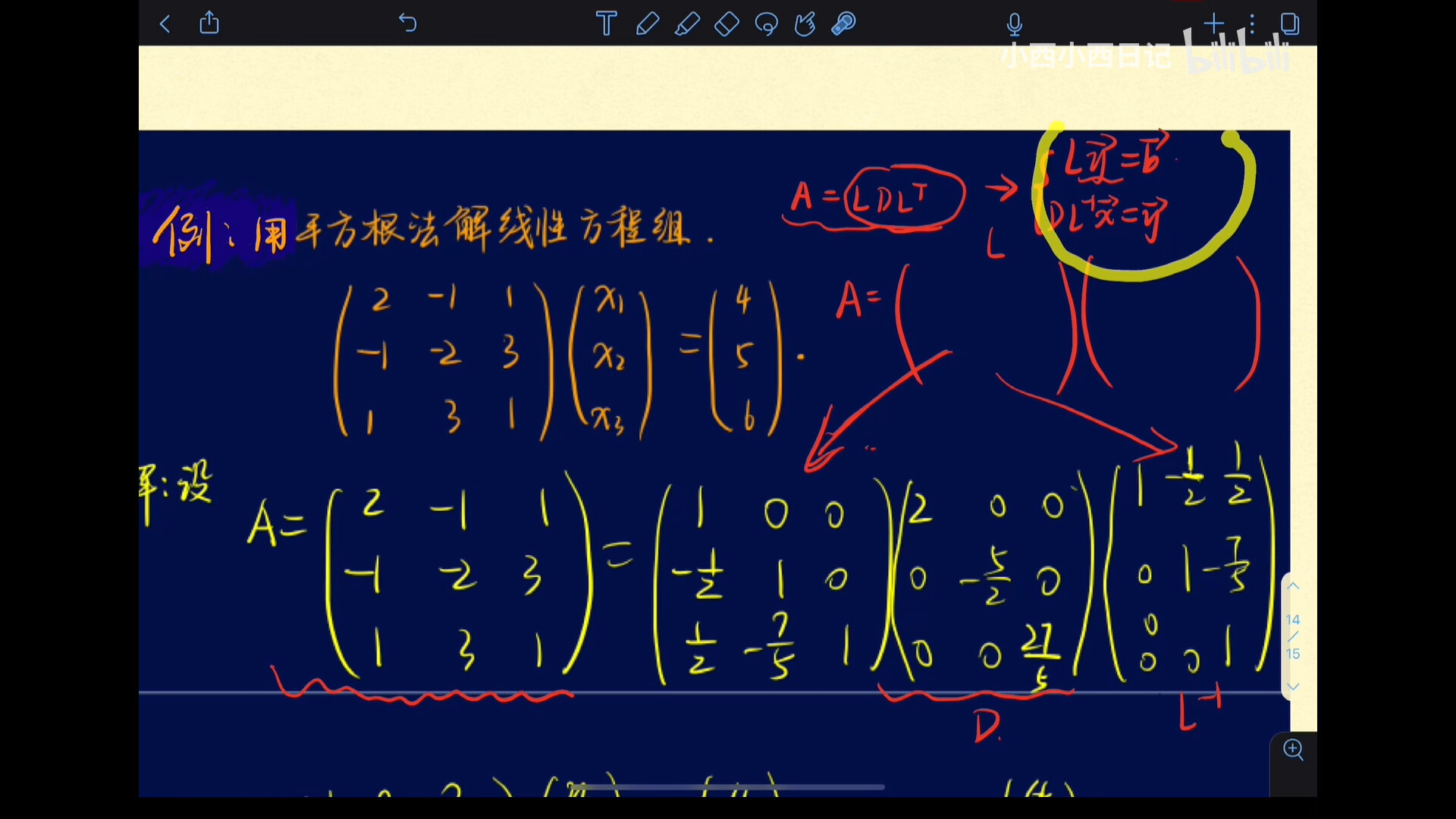
image-20220925203753719

计算时首先分解为A=LU的形式再转变为A=$LDL^T$的形式

其中：

  • L不变直接照抄
  • D的主对角线元素等同于U的主对角线元素
  • L转置得到$L^T$

之后按照正常方法求解，公式略有变化
$$
\begin{cases}
Ly = b \
DL^Tx = y \
\end{cases}
$$
image-20220925204052092

计算时可将两边同时左乘一个D的逆，将D移到等式右边运算，简化计算

追赶法

【数值分析】矩阵三角分解｜速成平方根法和追赶法 解线性方程组_哔哩哔哩_bilibili

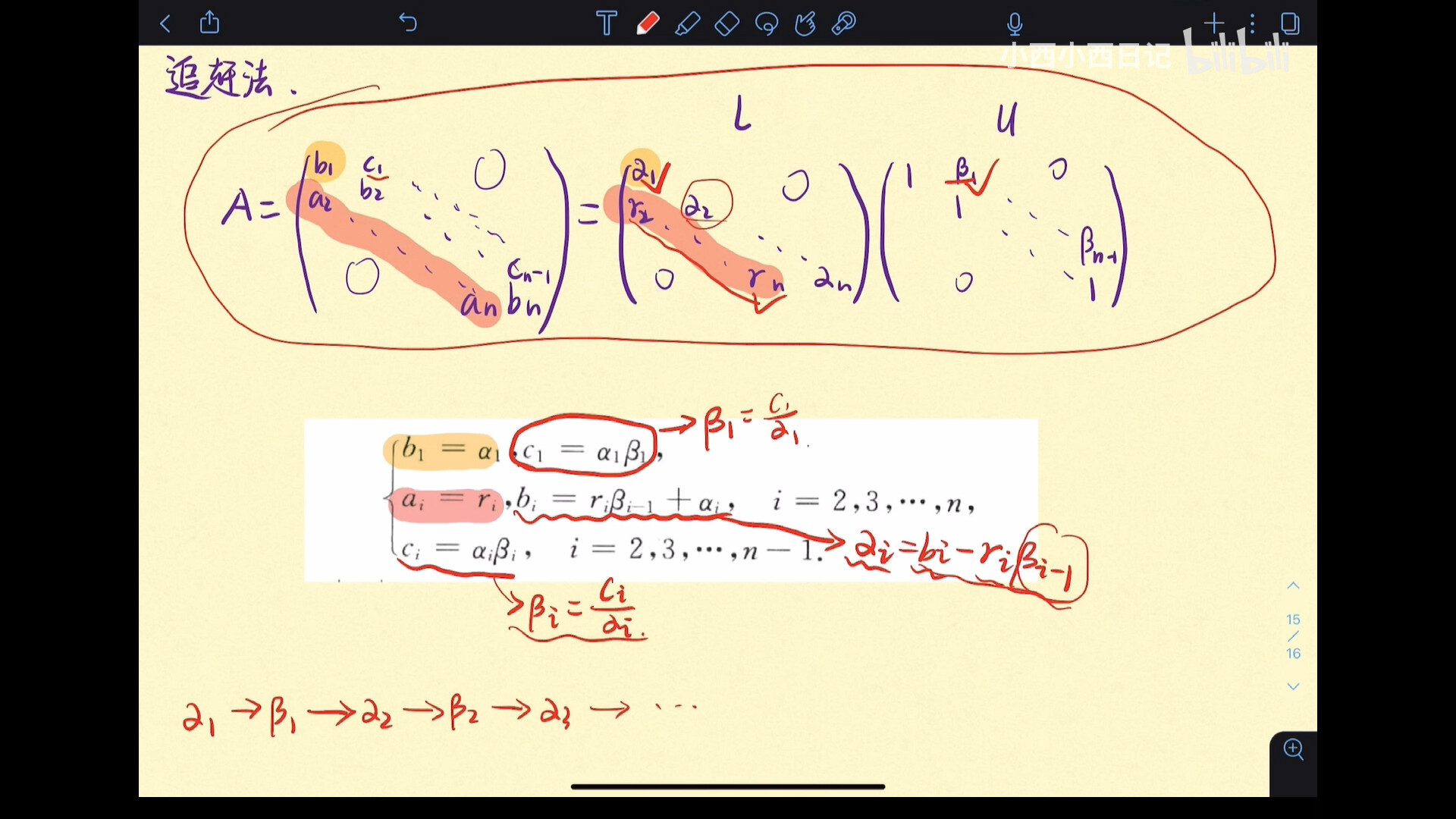
image-20220925204231441

对形如这样的三对角线方程组，采用追赶法计算

  • 首先根据公式得出L的$a_{11}$和下方的一条斜对角线
  • 依次计算图中的$\beta_1$、$\alpha_2$、$\beta_2$、$\alpha_3$等等

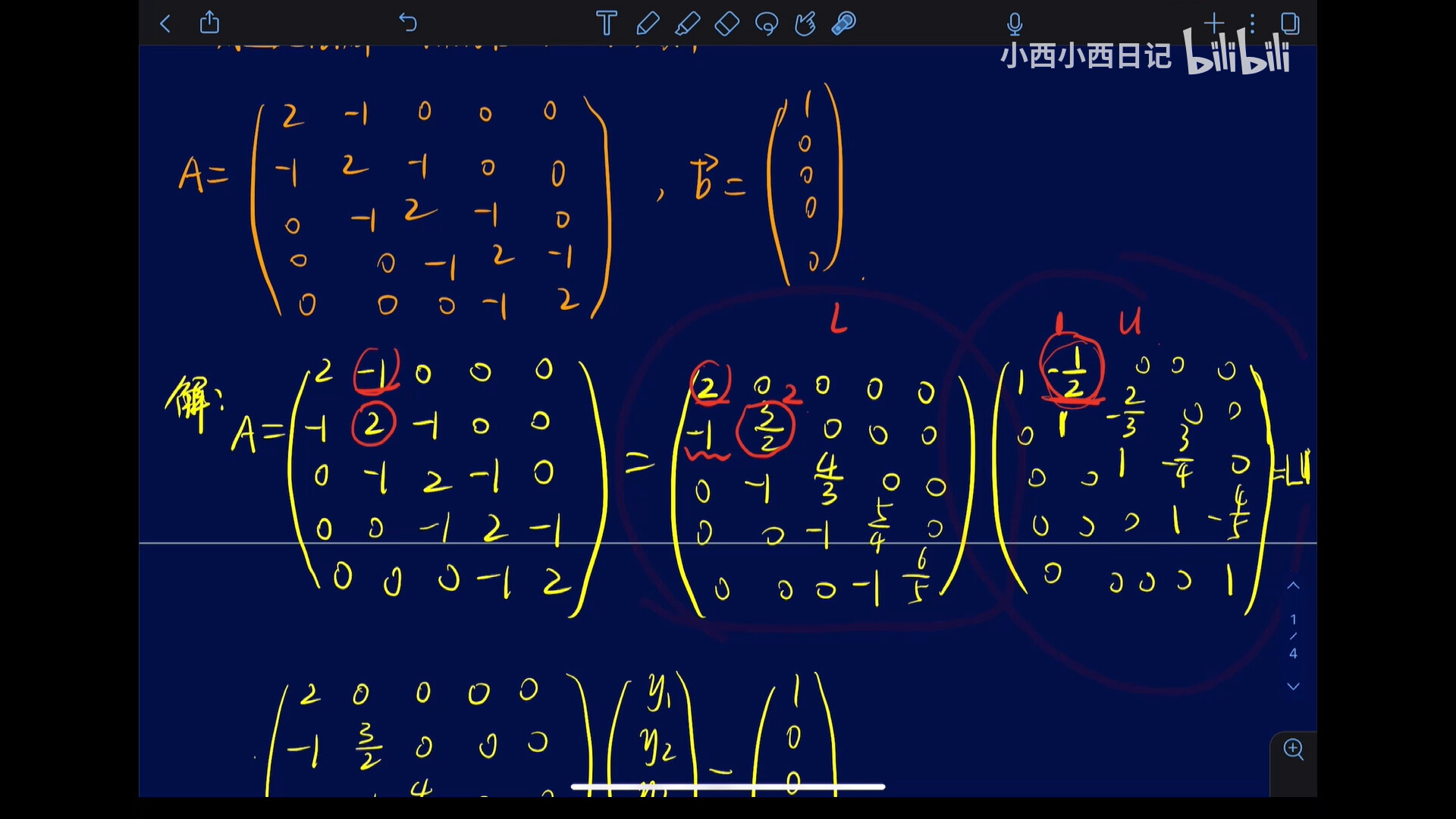
image-20220925204542988

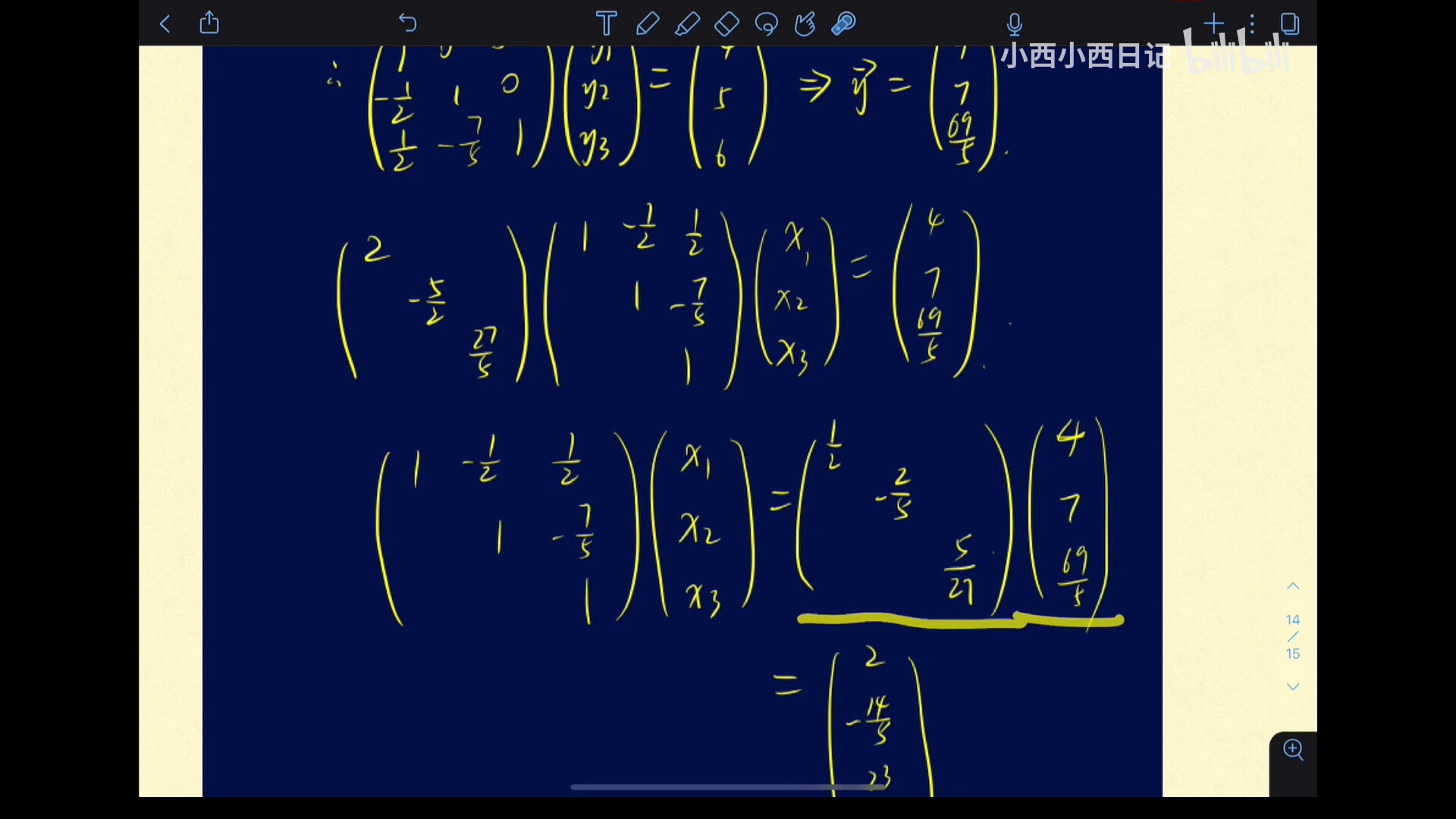
将结果依次求出，其中：

  • $-\frac{1}{2} = 2 \div -1$
  • $\frac{3}{2} = 2 - (-1) \times (-\frac{1}{2})$
  • $-\frac{2}{3} = -1 \div \frac{3}{2}$

规律为：

  • L中的未知量，即主对角线元素，为A中同位置元素，减去L中左方元素和左上方元素的乘积
  • U中的未知量，即主对角线上的对角线元素，为A中同位置元素，除以L中同位置的左方元素，也是上一步求得的结果

算出L和U以后，按照常规方法求出未知数
$$
\begin{cases}
Ly = b \
L^Tx = y \
\end{cases}
$$

解线性方程组的迭代法

向量和矩阵的范数

数值分析 范数与条件数 期末干货 期末突击_哔哩哔哩_bilibili

矩阵论（第五章）向量，矩阵的范数-期末快速复习_哔哩哔哩_bilibili

数值分析 计算矩阵特征值及谱半径 保姆教程_哔哩哔哩_bilibili

向量范数

image-20220926145442316

矩阵范数

$

谱半径

谱半径$f(A)$为矩阵的特征值的绝对值的最大值

小结

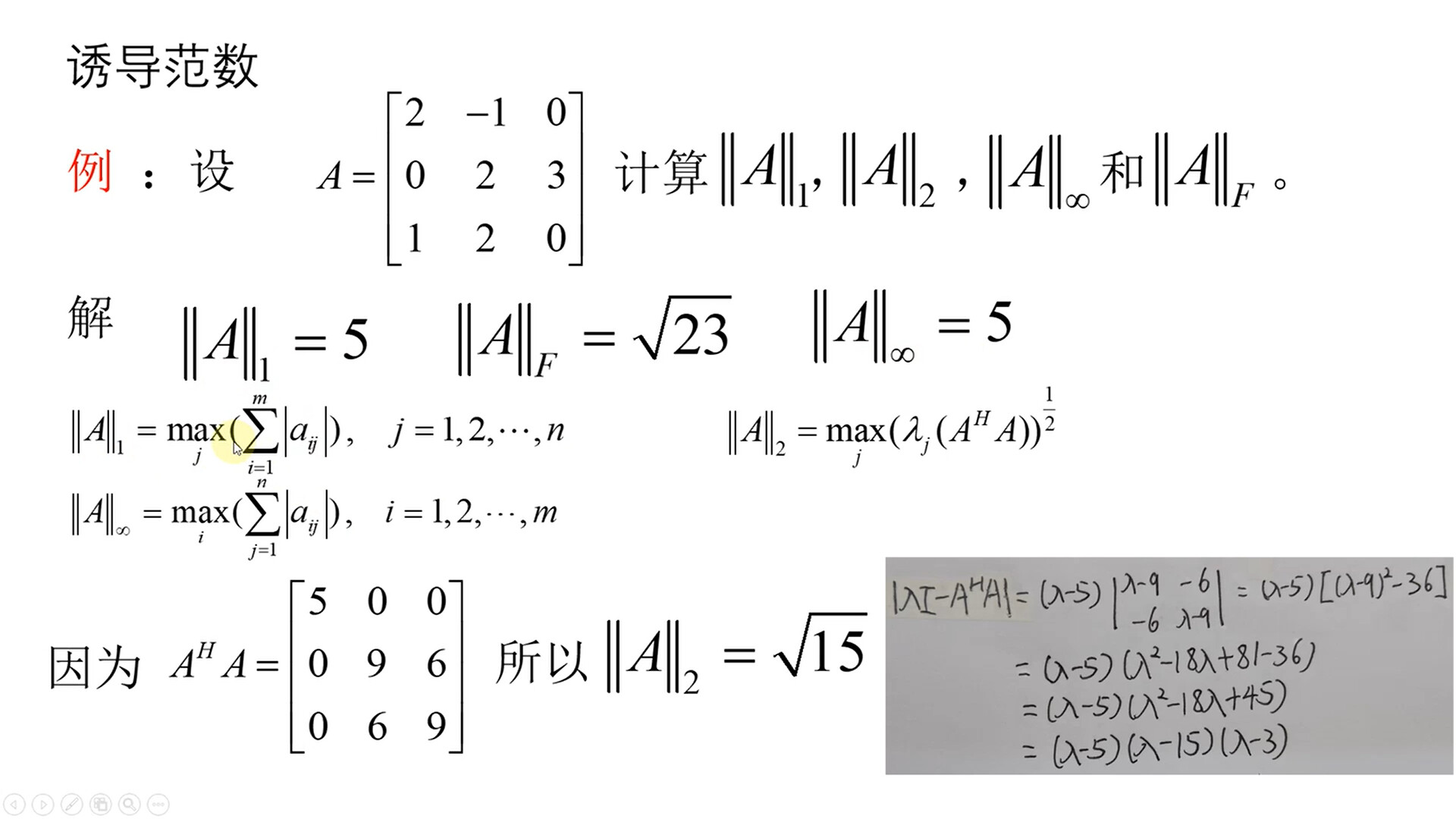
image-20220926145806381

  • 向量/矩阵的1范数都是求取列的绝对值之和，找出其中的最大值
  • 向量/矩阵的无穷范数都是求取行的绝对值之和，找出其中的最大值
  • 向量的2范数为每个元素的平方和开根号
  • 矩阵的2范数需要求出$A^TA$矩阵的特征值，选取其中的最大值

image-20220926150448690

线性方程组的误差分析

条件数

数值分析 范数与条件数 期末干货 期末突击_哔哩哔哩_bilibili

image-20220926150558219

条件数$cond(A)_x$对应了范数$||A||_x||A^{-1}_x||$的乘积

矩阵求逆

上图中逆矩阵结果错误

二阶矩阵求逆可参考下面的公式

img

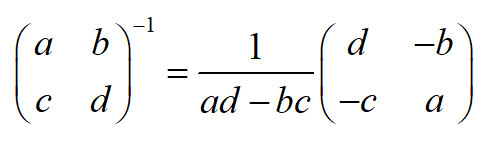
更高阶的求逆法：求逆矩阵的三种方法 - 哔哩哔哩 (bilibili.com)

雅各比方法和高斯-赛德尔方法

【数值分析】速成！雅可比迭代｜高斯赛德尔迭代_哔哩哔哩_bilibili

数值分析|雅可比和高斯迭代|期末干货|期末突击_哔哩哔哩_bilibili

雅各比方法

image-20221009195103098

将给定的矩阵A拆解为$B = -D^{-1}(L+U)$，求解出$B$判断收敛：

  • 对角线绝对占优，充分非必要
  • 谱半径小于1
    • 矩阵的特征值的最大的绝对值一项

高斯-赛德尔方法

image-20221009195142372

将给定的矩阵A拆解为$G = -(L+D)^{-1}U$，求解出$G$判断收敛：

  • 谱半径小于1
    • 矩阵的特征值的最大的绝对值一项

求矩阵的特征值性质与归纳

  • 特征值之和等于矩阵的迹，即主对角线之和

  • 对形如

    • $$
      \left|
      \matrix{
      \lambda & -\frac{a}{n} & -\frac{b}{n} \
      \frac{a}{n} & \lambda & -\frac{c}{n} \
      \frac{b}{n} & \frac{c}{n} & \lambda \

      }
      \right|
      \Longrightarrow
      \lambda(\lambda^{2} + \frac{a^2 + b^2 + c^2}{n^2})=0
      $$

插值法

数值分析02-牛顿插值多项式（例题）Newton_哔哩哔哩_bilibili

数值分析01-拉格朗日插值多项式及其余项（例题）Lagrange_哔哩哔哩_bilibili

牛顿插值多项式

公式

$$
N_n(x) = y_0 + c_1(x-x_0) + c_2(x-x_0)(x-x_1) + c_3(x-x_0)(x-x_1)(x-x_2) + …
$$

其中$c_n$为差商

差商表

以

  • 1,1
  • 2,4
  • 3,7
  • 4,8

根据所给定数表求取差商表的过程：

$k$ $x_k$ $f(x_k)$ $c_1$ $c_2$ $c_3$
0 1 1
1 2 4 $\frac{4-1}{2-1}=3$
2 3 7 $\frac{7-4}{3-2}=3$ $\frac{3-3}{3-1}=0$
3 4 8 $\frac{8-7}{4-3}=1$ $\frac{1-3}{4-2}=-1$ $\frac{0+1}{4-1}=\frac{1}{3}$

由此就可求多次牛顿差值多项式了

拉格朗日插值多项式

公式

以二次为例：
$$
\begin{aligned}
L_2(X)
&= l_0(x)y_0 + l_1(x)y_1 + l_2(x)y_2 \
&= \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}y_0 + \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}y_1 + \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}y_2
\end{aligned}
$$

插值多项式的误差/插值余项

无论是牛顿插值多项式还是拉格朗日插值多项式都存在误差，设其为$P_n(x)$，则对于插值余项$R_n(x)$：
$$
\begin{aligned}
R_n(x)
&= f(x) - P_n(x)\
&= \frac{f^{n+1}(\varepsilon)}{(n+1)!}W_{n+1}(x)
\end{aligned}
$$
其中
$$
W_{n+1}(x) = (x-x_0)(x-x_1)…(x-x_n)
$$
也可表示为：

$$
\begin{aligned}
|R_n(x)|
&\leq \frac{M_{n+1}}{(n+1)!}W_{n+1}(x)
\end{aligned}
$$

其中
$$
M_{n+1} = max|f^{n+1}(x)|,x_0 \leq x \leq x_n
$$
写题使用第二种方法，通过函数的特定次导数的最大绝对值求取插值余项

image-20221009213831764

差商与导数之间的关系

image-20221009214742097

则可知使用五个点时就可得到完全精确的插值多项式了

如若导数中存在未知量$x$，则可用之前的方法计算差商

曲线拟合与函数逼近

曲线拟合的最小二乘法

三种求解方法

法一：

以

一 二 三
X 1 2 3
Y 5 9 16

进行最小二乘法拟合的一次多项式：

设$p(x)=ax+b$，则
$$
\begin{aligned}
S
&= \sum_{i=1}^{3}[p(x_i)-y_i]^2\
&= (a+b-5)^2 + (2a+b-9)^2 + (3a+b-16)^2
\end{aligned}
$$
之后通过偏导为0求取$a、b$：

$$
\begin{cases}
\frac{\delta S}{\delta a} = 0 \
\frac{\delta S}{\delta b} = 0
\end{cases}
$$
法二：

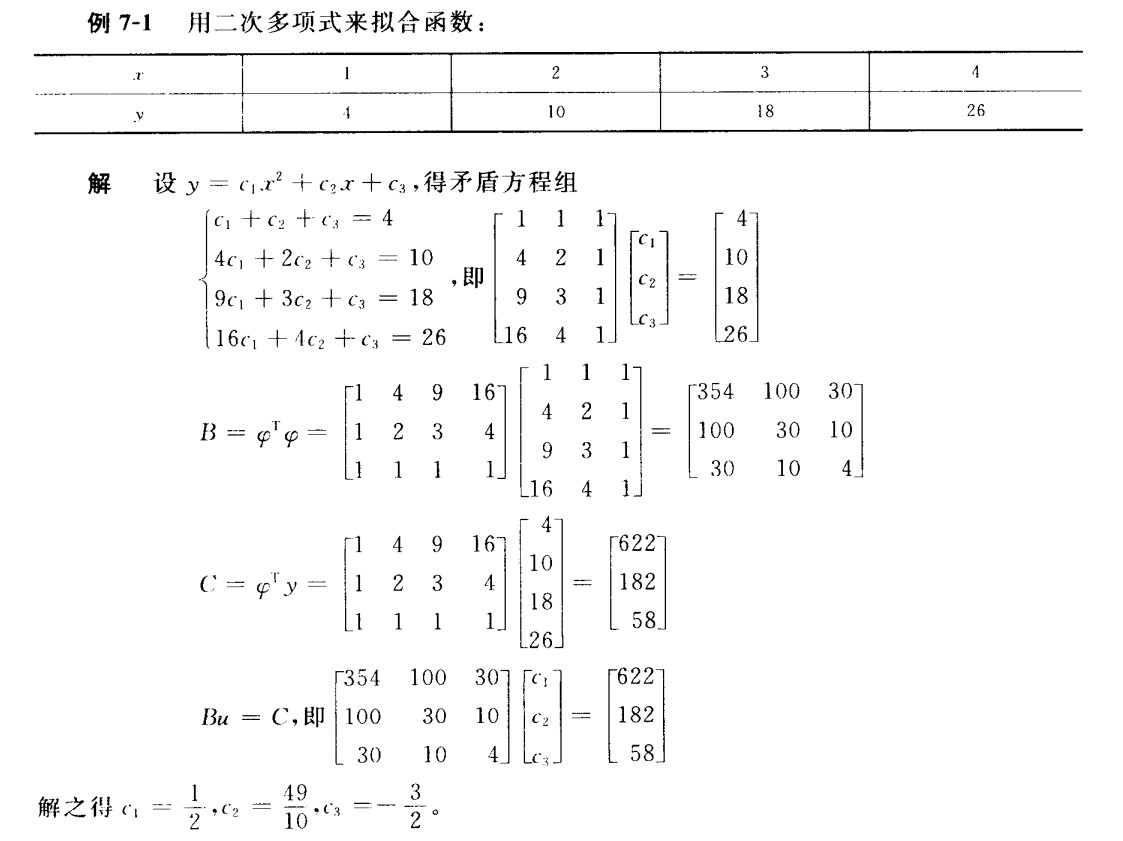
image-20221010005703785

法三：

数值分析【题型六】最小二乘法求拟合曲线，均方误差的例题详解_哔哩哔哩_bilibili

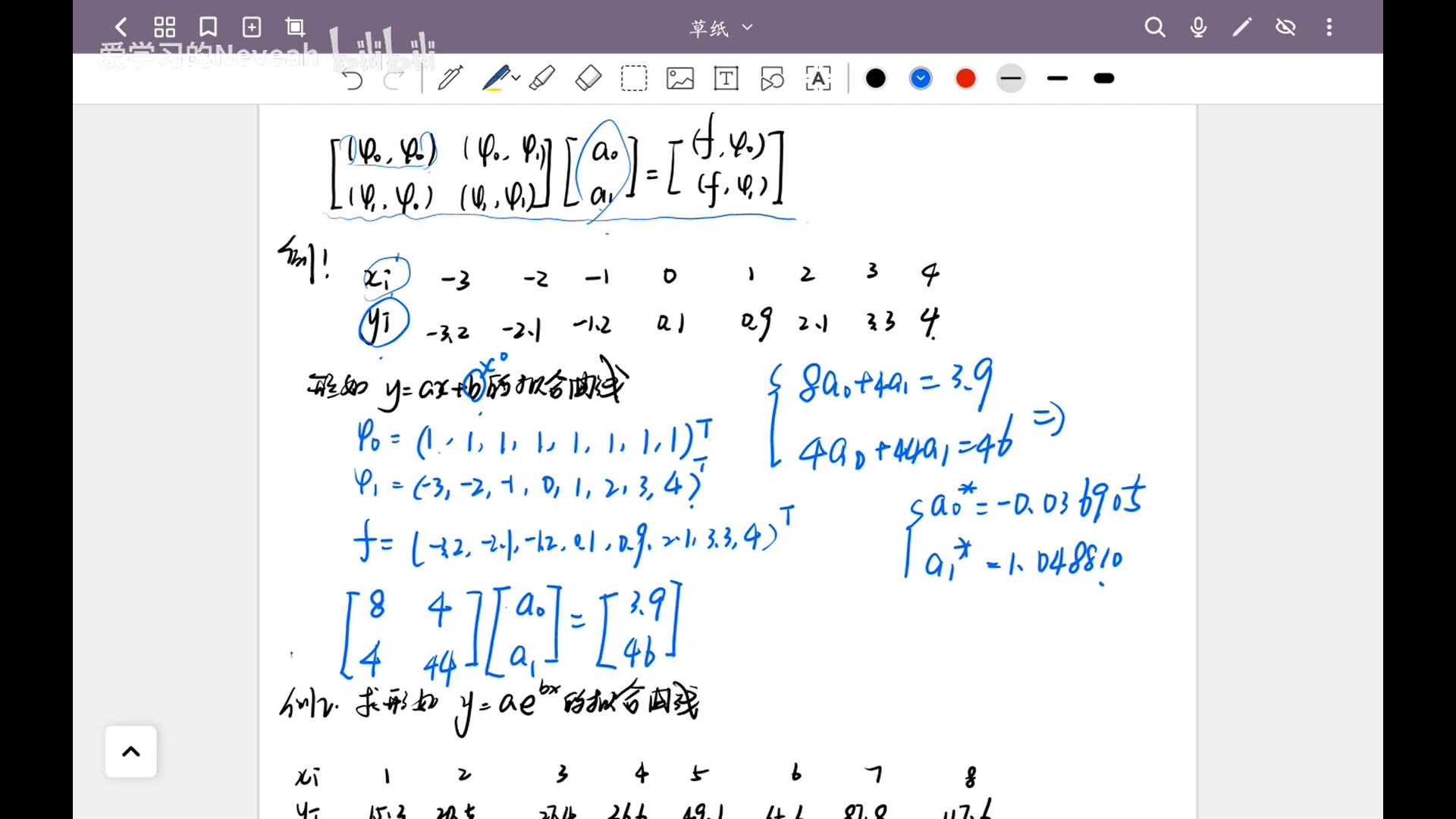
image-20221010013215792

使用公式：
$$
\left[
\matrix
{
(\phi_0,\phi_0) & (\phi_0,\phi_1)\
(\phi_1,\phi_0) & (\phi_1,\phi_1)
}
\right]
\left[
\matrix
{
a_0\
a_1
}
\right]
=
\left[
\matrix
{
(f,\phi_0)\
(f,\phi_1)
}
\right]
$$
其中

  • $\phi_0、\phi_1$对应$x_i$的0、1次方
  • $f$对应$y_i$
  • $a_i$为系数，即分别为$b、a$
  • 内积的求取方式为对应位置元素乘积后求和

权

虽然都是离散的数据点，但有些点可能是多次测量的，那么就需要提高它在拟合时的占比

image-20221010010033655

对于第三行的$w_i$，即为权

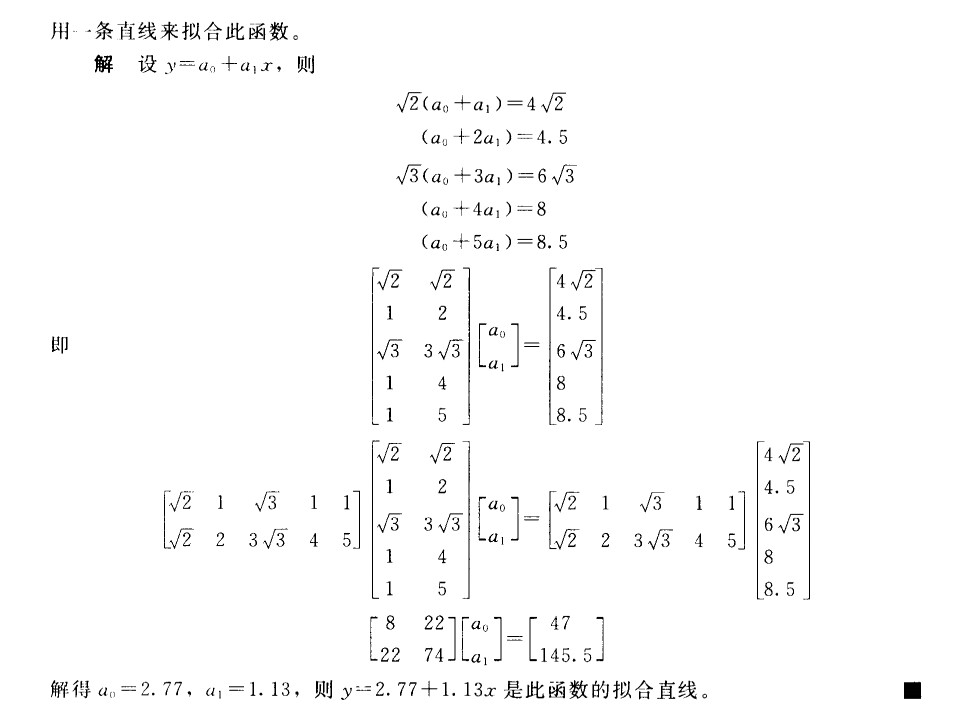
image-20221010010059171

在构造矛盾方程组时，只需要等式两边同时乘上$\sqrt{w_i}$，之后正常计算即可

用正交函数作最小二乘拟合

求解方法

有递推公式：
$$
\begin{aligned}
&p_0(x) = 1\
&p_1(x) = (x-\alpha_1)p_0(x)\
&p_{k+1}(x) = (x-\alpha_{k+1})p_k(x)-\beta_kp_{k-1}(x)
\end{aligned}
$$
由正交性可定义：
$$
\begin{aligned}
&\alpha_{k+1} = \frac{(xp_k,p_k)}{(p_k,p_k)}\
&\beta_{k} = \frac{(xp_k,p_{k-1})}{(p_{k-1},p_{k-1})}\
&c_k = \frac{(f,p_{i-1})}{(p_{i-1},p_{i-1})}
\end{aligned}
$$

例题

image-20221010103219549

image-20221010103244891